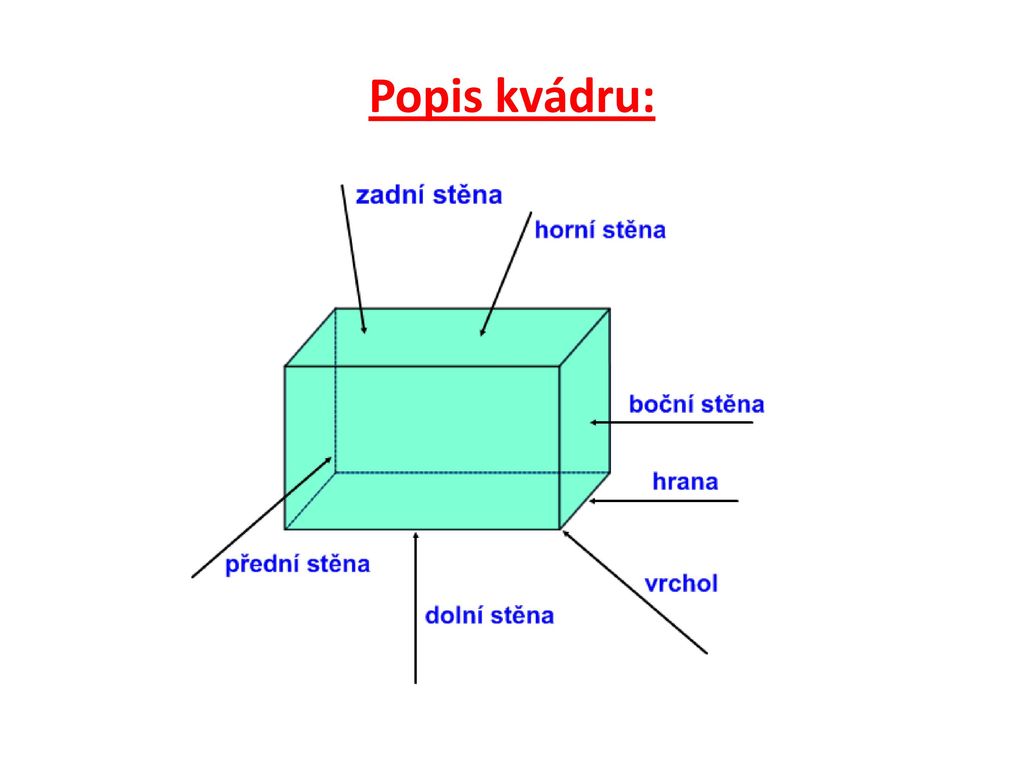
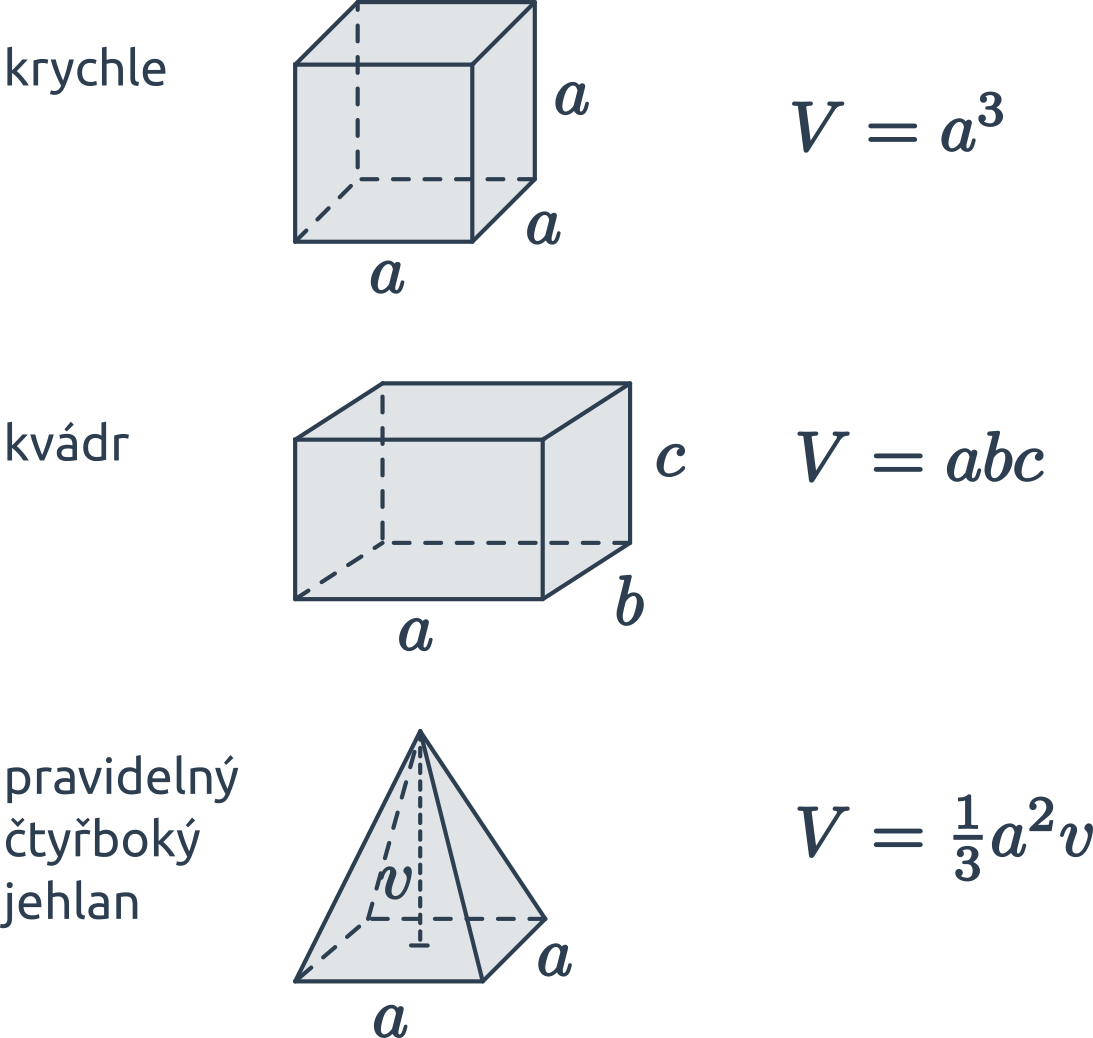
U kvádru můžou být všechny tři rozměry různé (délka, šířka a výška), proto těmto rozměrům obecně přiřazujeme tři různá písmenka – „a, b, c“. Objem kvádru vypočítáme tak, že spočteme obsah podstavy (obdélník – S=a.b), kterou dále vynásobíme výškou kvádru (c). Výsledná hodnota je v objemových jednotkách.Krychle je geometrické těleso, které má tři rozměry. Skládá se ze šesti navzájem shodných čtverců. Kvádr je geometrické těleso, které má tři rozměry. Skládá se ze šesti obdélníků, přičemž každé dva obdélníky, které jsou proti sobě jsou shodné.Kvádr je prostorové těleso, jehož podstavou je čtverec nebo obdélník a boční stěny jsou kolmé na podstavu. Dvě protější stěny jsou stejné. Kvádr má osm vrcholů, dvanáct hran, šest stěn, dvanáct stěnových úhlopříček, čtyři tělesové úhlopříčky.

Co je objem kvádru : Objem kvádru je tedy součin délek jeho hran: V = a b c V = abc V=abc. Objem krychle vypočítáme stejným způsobem. Protože v krychli jsou všechny hrany stejně dlouhé, výraz se zjednoduší na V = a 3 V = a^3 V=a3.

Kolik má Kvadr podstav

KVÁDR. Za kvádr považujeme kolmý hranol, jehož podstavou je obdélník nebo čtverec. Tudíž se jedná o čtyřboký hranol. V případě, že podstavy kvádru jsou čtverce, jedná se o pravidelný čtyřboký hranol.

Jak Vypocitat podstavu krychle : U krychle jsou všechny tři rozměry stejné (délka, šířka a i výška), proto všem rozměrům u tohoto tělesa obecně přiřazujeme jedno písmenko – „a“. Objem krychle vypočítáme tak, že spočteme obsah podstavy (čtverec – S=a.a), kterou dále vynásobíme výškou krychle (a). Výsledná hodnota je v objemových jednotkách.

Kvádr má tři rozměry: šířku, délku a výšku, které nemusí být stejné, jako je tomu u krychle. Kvádr má šest stěn, tvar každé stěny je obdélník nebo čtverec, pokud jsou všechny stěny tvaru čtverce, jde o krychli. Příklady kvádrů v běžném životě zahrnují krabice, knihy nebo cihly.

Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.

Jak vypočítat m2 kvádru

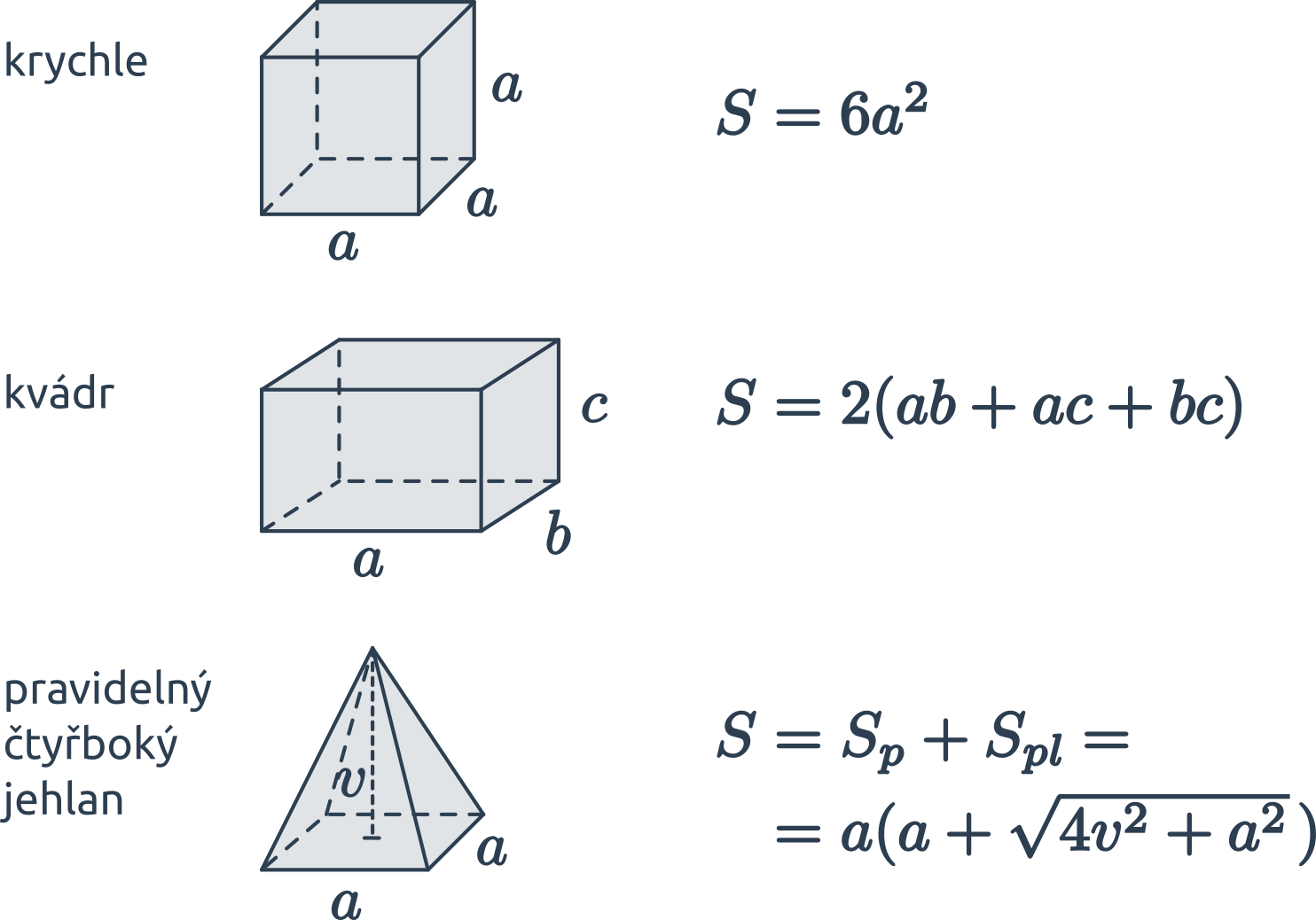
Jak vypočítat povrch krychle Kvádr má šest stěn a všechny jsou tvořené obdélníky, vždy dvě jsou stejně velké. Povrch kvádru vypočítáme jako: S = 2(ab + bc + ac).V každé stěně jsou dvě stěnové úhlopříčky, všechny jsou stejně dlouhé.Základní vzorce

1. Průměr: d = 2 × r.
2. Poloměr: r = d / 2.
3. Obvod podstavy: O = π d = 2 π r.
4. Plocha podstavy kužele: P = π d2 / 4 = π r2
5. Délka boční stěny: b = √ (r2 + h2)
6. Plocha pláště kužele: Q = O × b / 2 = π r b.
7. Celkový povrch/plocha kužele: S = P + Q = π r2 + π r b = π r (r + b)

Výška v kvádru je rovna trojnásobku délky kratšího rozměru podstavy.

Kolik má kvádr podstav : KVÁDR. Za kvádr považujeme kolmý hranol, jehož podstavou je obdélník nebo čtverec. Tudíž se jedná o čtyřboký hranol.

Kolik stran má kvádr :

Kvádr
Počet vrcholů	8
Počet hran	12
Počet stěn	6
Úhel u vrcholu	90°

Jaký je rozdíl mezi hranolem a kvádrem

Hranol – čtverec, kvádr – obdélník. Kvádr má po obvodu 6 stejných čtverců. Hranol může mít jako podstavu čtverce (i protilehlá strana je čtverec) a boční 4 strany obdélníky. Může ale mít jako podstavu obdélník a protilehlá strana stejný obdélník.

Vzorec: Stěna = délka * výška. Strop = délka * šířka. Plocha stěny se vypočítá vynásobením obou délek. Například stěna, která má délku 5 metrů a výšku 2,5 metru má plochu 12,5 m2: 5 * 2,5 = 12,5.

1. Obsah podstavy kužele: π r 2 \pi r^2 πr2.
2. Obsah pláště kužele: 1 2 ⋅ 2 π r ⋅ s = π r s \frac{1}{2} \cdot 2 \pi r \cdot s = \pi r s 21⋅2πr⋅s=πrs.

Jak se pocita Kuzelovitost : Kuželovitost se vyjadřuje obecně poměrem 1 : x – což znamená, že na délce x (mm) se průměr změní o 1 mm. Soustružník si vypočítá kuželovitost nebo sklon a z nich potom úhel sklonu kužele (/2). Kuželovitost se na výkrese připisuje k ose kužele a sklon k povrchové úsečce.