Trajektorie (též pohybová křivka) je geometrická čára prostorem, kterou hmotný bod nebo těleso při pohybu opisuje. Jedná se tedy o množinu všech poloh (hmotného) bodu, v nichž se může v různých časových okamžicích nacházet. Trajektorie s vyznačením bodů v různých časových okamžicích.Dráha. Ve fyzice označuje dráha délku trajektorie, kterou těleso (hmotný bod) urazí za určitou dobu. Dráha je tedy vzdálenost, kterou těleso (hmotný bod) urazí mezi dvěma časovými okamžiky a měří se podél trajektorie. Dráha je charakteristikou mechanického pohybu.Zvláštním případem jsou zde trajektorie ve tvaru kružnic (již zmíněný pohyb Země kolem Slunce), kdy hovoříme o pohybu hmotného bodu po kružnici (resp. o pohybu po kružnici). Délka trajektorie, kterou hmotný bod opíše za určitý čas t, se nazývá dráha. Značí se s a její základní jednotkou je metr, což lze zapsat takto .

Jaké máme druhy pohybu : Rozlišujeme několik typů mechanického pohybu:

• přímočarý pohyb. posuvný pohyb.
• křivočarý pohyb. šroubový pohyb. pohyb po kružnici. rovnoměrný pohyb po kružnici. nerovnoměrný pohyb po kružnici. otáčivý pohyb, otáčení, (rotace) valivý pohyb. smykový pohyb.

Jak se značí trajektorie

délka trajektorie opsaná tělesem za určitou dobu ● je to fyzikální veličina, značí se písmenem s ● udává a měří se v jednotkách délky (m, cm, km…)

Jak se dělí trajektorie : Podle tvaru trajektorie dělíme pohyb na přímočarý a křivočarý. Přímočarý pohyb je rovný pohyb. Přímočarý pohyb dělá například těleso, které padá rovně k zemi, auto na rovné dálnici. Trajektorie přímočarého pohybu je rovná čára (úsečka).

Trajektorie je objekt, totiž (myšlená) čára, která popisuje pohyb bodu. Jako příklad můžeme uvést stopu za lyžařem, červenou nit v Minotaurově labyrintu, nebo stopu na papíře, kterou zanechává při psaní naše ruka. Dráha je veličina, tedy vlastnost trajektorie – její délka.

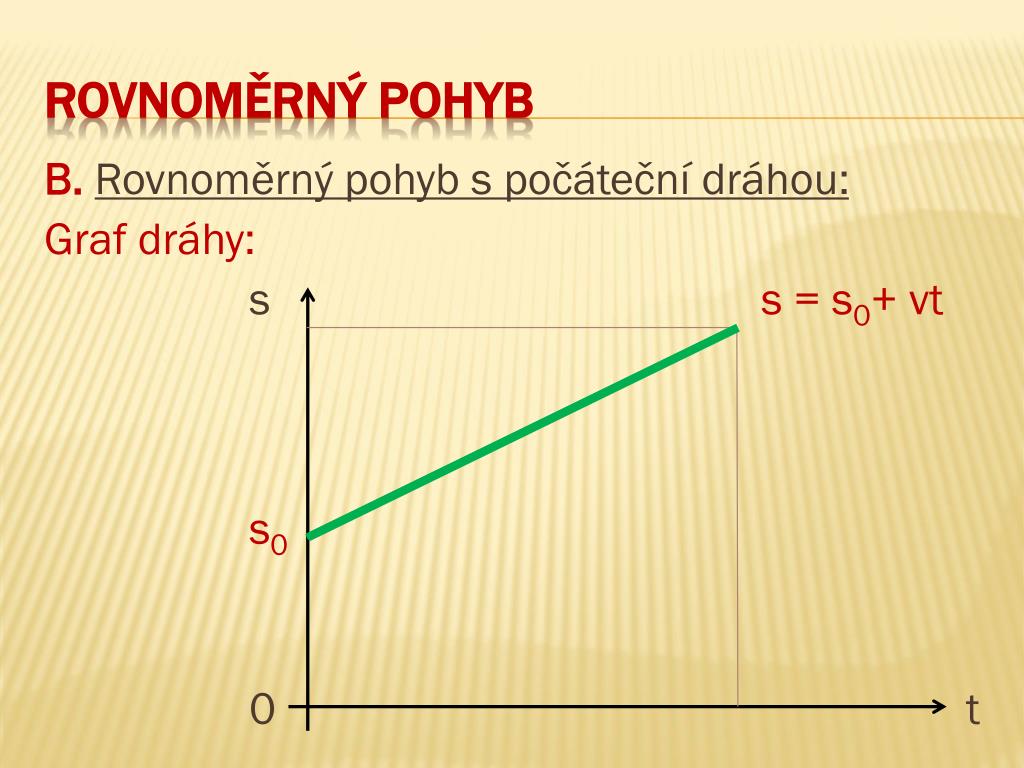
Dráha rovnoměrného pohybu odpovídá v grafu časového průběhu rychlosti obsahu obdélníku. I z grafického znázornění je patrné, že dráha tělesa bude větší, když se bude těleso pohybovat rychleji nebo delší dobu. Vzorec s = v · t platí jen při rovnoměrném pohybu tělesa.

Co je to trajektorie pohybu

Při pohybu tělesa se mění jeho souřadnice vzhledem ke zvolené souřadné soustavě v závislosti na čase. Geometrická čára, kterou těleso při pohybu opisuje, se nazývá trajektorie. Podle trajektorie dělíme pohyby na přímočaré a křivočaré (zvláštním případem je pohyb po kružnici).Pohyb dělíme na rovnoměrný a nerovnoměrný podle toho, jestli se mění velikost rychlosti. U tohoto dělení naopak nezáleží na tom, jestli se mění směr pohybu (směr rychlosti).Některá pohybující se tělesa za sebou zanechávají stopu, tu nazýváme trajektorie tělesa. Délka trajektorie se nazývá dráha.

Trajektorie je objekt, totiž (myšlená) čára, která popisuje pohyb bodu. Jako příklad můžeme uvést stopu za lyžařem, červenou nit v Minotaurově labyrintu, nebo stopu na papíře, kterou zanechává při psaní naše ruka. Dráha je veličina, tedy vlastnost trajektorie – její délka.

Jaký je vzoreček pro rychlost : Použijeme vzorec v = s t v=\frac{s}{t} v=ts​, ale přímo známe jen čas t t t.

Jak dělíme pohyby podle trajektorie : Podle tvaru trajektorie dělíme pohyb na přímočarý a křivočarý.

Co Rozumime drahou pohybu tělesa

Těleso se pohybuje, mění – li svou polohu vzhledem k jinému tělesu. Totéž těleso může být v pohybu vzhledem k jednomu tělesu a současně v klidu vzhledem k druhému tělesu. Čára, kterou při pohybu těleso opisuje, se nazývá trajektorie pohybu tělesa.

Okamžitá velikost rychlosti je velikost rychlosti tělesa v určitém časovém okamžiku. Pokud k té velikosti rychlosti přidáte směr, dostanete okamžitou rychlost.Dráha rovnoměrného pohybu odpovídá v grafu časového průběhu rychlosti obsahu obdélníku. I z grafického znázornění je patrné, že dráha tělesa bude větší, když se bude těleso pohybovat rychleji nebo delší dobu. Vzorec s = v · t platí jen při rovnoměrném pohybu tělesa.

Jak vypočítat čas kdyz znam rychlost a drahu :

1. Souvislost rychlosti, dráhy a času. Známe-li průměrnou rychlost v a celkový čas t, můžeme vypočítat dráhu s takto:
2. dráha = rychlost . čas. s = v . t.
3. rychlost = dráha : časem. v = s : t. Známe-li průměrnou rychlost v a celkovou dráhu s, můžeme vypočítat čas t takto:
4. s. s=v.t. m, km. čas.
5. t. t=s:v. s, h. rychlost.